Example of a Run of Genetic Programming
(Symbolic Regression of a Quadratic Polynomial)
This page describes an illustrative run of genetic programming in which the goal is to automatically create a computer program whose output is equal to the values of the quadratic polynomial x2+x+1 in the range from –1 to +1. That is, the goal is to automatically create a computer program that matches certain numerical data. This process is sometimes called system identification or symbolic regression.
We begin with the five preparatory steps for the problem and then proceed to the executional steps of the run of genetic programming.
Preparatory Steps
The purpose of the first two preparatory steps is to specify the ingredients of the to-be-evolved program.
Because the problem is to find a mathematical function of one independent variable, the terminal set (inputs to the to-be-evolved program) includes the independent variable, x. The terminal set also includes numerical constants. That is, the terminal set, T, is
T = {X, Â},
where  denotes constant numerical terminals in some reasonable range (say from –5.0 to +5.0).
The preceding statement of the problem is somewhat flexible in that it does not specify what functions may be employed in the to-be-evolved program. One possible choice for the function set consists of the four ordinary arithmetic functions of addition, subtraction, multiplication, and protected division. This choice is reasonable because mathematical expressions typically include these functions. Thus, the function set, F, for this problem is
F = {+, -, *, %}.
The two-argument +, -, *, and % functions add, subtract, multiply, and divide, respectively. The protected division function % returns a value of 1 when division by 0 is attempted (including 0 divided by 0), but otherwise returns the quotient of its two arguments.
Each individual in the population is a composition of functions from the specified function set and terminals from the specified terminal set.
The third preparatory step involves constructing the fitness measure. The purpose of the fitness measure is to specify what the human wants. The high-level goal of this problem is to find a program whose output is equal to the values of the quadratic polynomial x2+x+1. Therefore, the fitness assigned to a particular individual in the population for this problem must reflect how closely the output of an individual program comes to the target polynomial x2+x+1. The fitness measure could be defined as the value of the integral (taken over values of the independent variable x between –1.0 and +1.0) of the absolute value of the differences (errors) between the value of the individual mathematical expression and the target quadratic polynomial x2+x+1. A smaller value of fitness (error) is better. A fitness (error) of zero would indicate a perfect fit.
For most problems of symbolic regression or system identification, it is not practical or possible to analytically compute the value of the integral of the absolute error. Thus, in practice, the integral is numerically approximated using dozens or hundreds of different values of the independent variable x in the range between –1.0 and +1.0.
The population size in this small illustrative example will be just four. In actual practice, the population size for a run of genetic programming consists of thousands or millions of individuals. In actual practice, the crossover operation is commonly performed on about 90% of the individuals in the population; the reproduction operation is performed on about 8% of the population; the mutation operation is performed on about 1% of the population; and the architecture-altering operations are performed on perhaps 1% of the population. Because this illustrative example involves an abnormally small population of only four individuals, the crossover operation will be performed on two individuals and the mutation and reproduction operations will each be performed on one individual. For simplicity, the architecture-altering operations are not used for this problem.
A reasonable termination criterion for this problem is that the run will continue from generation to generation until the fitness of some individual gets below 0.01. In this contrived example, the run will (atypically) yield an algebraically perfect solution (for which the fitness measure attains the ideal value of zero) after merely one generation.
Click here for additional information about the preparatory steps of a run of genetic programming.
Executional Steps
One the human user has performed the five preparatory steps, the run of genetic programming can be launched. That is, the executional steps shown in the flowchart of genetic programming are performed.
Genetic programming starts by randomly creating a population of four individual computer programs. The four programs are shown in figure 1 in the form of trees.
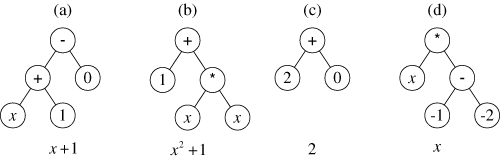
Figure 1 Initial population of four randomly created individuals of
generation 0

Figure 2 The fitness of each of the four randomly created individuals of
generation 0 is equal to the area between two curves
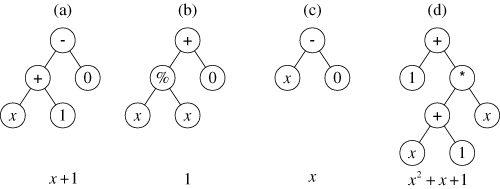
Figure 3 Population of generation 1 (after one reproduction, one
mutation, and one two-offspring crossover operation)
The first randomly constructed program tree (figure 1a) is equivalent to the mathematical expression x+1. A program tree is executed in a depth-first way, from left to right, in the style of the LISP programming language. Specifically, the addition function (+) is executed with the variable x and the constant value 1 as its two arguments. Then, the two-argument subtraction function (–) is executed. Its first argument is the value returned by the just-executed addition function. Its second argument is the constant value 0. The overall result of executing the entire program tree is thus x+1.
The first program (figure 1a) was constructed by first choosing the subtraction function for the root (top point) of the program tree. The random construction process continued in a depth-first fashion (from left to right) and chose the addition function to be the first argument of the subtraction function. The random construction process then chose the terminal x to be the first argument of the addition function (thereby terminating the growth of this path in the program tree). The random construction process then chose the constant terminal 1 as the second argument of the addition function (thereby terminating the growth along this path). Finally, the random construction process chose the constant terminal 0 as the second argument of the subtraction function (thereby terminating the entire construction process).
The second program (figure 1b) adds the constant terminal 1 to the result of multiplying x by x and is equivalent to x2+1. The third program (figure 1c) adds the constant terminal 2 to the constant terminal 0 and is equivalent to the constant value 2. The fourth program (figure 1d) is equivalent to x.
Randomly created computer programs will, of course, typically be very poor at solving the problem at hand. However, even in a population of randomly created programs, some programs are better than others. The four random individuals from generation 0 in figure 1 produce outputs that deviate from the output produced by the target quadratic function x2+x+1 by different amounts. In this contrived illustrative problem, fitness can be graphically illustrated as the area between two curves. That is, fitness is equal to the area between the parabola x2+x+1 and the curve representing the candidate individual. Figure 2 shows (as shaded areas) the integral of the absolute value of the errors between each of the four individuals in figure 1 and the target quadratic function x2+x+1. The integral of absolute error for the straight line x+1 (the first individual) is 0.67 (figure 2a). The integral of absolute error for the parabola x2+1 (the second individual) is 1.0 (figure 2b). The integral of the absolute errors for the remaining two individuals are 1.67 (figure 2c) and 2.67 (figure 2d), respectively.
As can be seen in figure 2, the straight line x+1 (figure 2a) is closer to the parabola x2+x+1 in the range from –1 to +1 than any of its three cohorts in the population. This straight line is, of course, not equivalent to the parabola x2+x+1. This best-of-generation individual from generation 0 is not even a quadratic function. It is merely the best candidate that happened to emerge from the blind random search of generation 0. In the valley of the blind, the one-eyed man is king.
After the fitness of each individual in the population is ascertained, genetic programming then probabilistically selects relatively more fit programs from the population. The genetic operations are applied to the selected individuals to create offspring programs. The most commonly employed methods for selecting individuals to participate in the genetic operations are tournament selection and fitness-proportionate selection. In both methods, the emphasis is on selecting relatively fit individuals. An important feature common to both methods is that the selection is not greedy. Individuals that are known to be inferior will be selected to a certain degree. The best individual in the population is not guaranteed to be selected. Moreover, the worst individual in the population will not necessarily be excluded. Anything can happen and nothing is guaranteed.
We first perform the reproduction operation. Because the first individual (figure 2.2a) is the most fit individual in the population, it is very likely to be selected to participate in a genetic operation. Let’s suppose that this particular individual is, in fact, selected for reproduction. If so, it is copied, without alteration, into the next generation (generation 1). It is shown in figure 2.4a as part of the population of the new generation.
We next perform the mutation operation. Because selection is probabilistic, it is possible that the third best individual in the population (figure 1c) is selected. One of the three points of this individual is then randomly picked as the site for the mutation. In this example, the constant terminal 2 is picked as the mutation site. This program is then randomly mutated by deleting the entire subtree rooted at the picked point (in this case, just the constant terminal 2) and inserting a subtree that is randomly grown in the same way that the individuals of the initial random population were originally created. In this particular instance, the randomly grown subtree (shown in figure 3b) computes the quotient of x and x using the protected division operation %. This particular mutation changes the original individual from one having a constant value of 2 into one having a constant value of 1. This particular mutation improves fitness from 1.67 to 1.00.
Finally, we perform the crossover operation. Because the first and second individuals in generation 0 are both relatively fit, they are likely to be selected to participate in crossover. In fact, because of its high fitness, the first individual ends up being selected twice to participate in a genetic operation. In contrast, the unfit fourth individual is not be selected at all. The reselection of relatively more fit individuals and the exclusion and extinction of unfit individuals is a characteristic feature of Darwinian selection. The first and second programs are mated sexually to produce two offspring (using the two-offspring version of the crossover operation). One point of the first parent (figure 1a), namely the + function, is randomly picked as the crossover point for the first parent. One point of the second parent (figure 1b), namely its leftmost terminal x, is randomly picked as the crossover point for the second parent. The crossover operation is then performed on the two parents. The two offspring are shown in figures 3c and 3d. One of the offspring (figure 3c) is equivalent to x and is not noteworthy. However, the other offspring (figure 3d) is equivalent to x2+x+1 and has a fitness (integral of absolute errors) of zero. Because the fitness of this individual is below 0.01, the termination criterion for the run is satisfied and the run is automatically terminated. This best-so-far individual (figure 3d) is designated as the result of the run. This individual is an algebraically correct solution to the problem.
Note that the best-of-run individual (figure 3d) incorporates a good trait (the quadratic term x2) from the second parent (figure 1b) with two other good traits (the linear term x and constant term of 1) from the first parent (figure 1a). The crossover operation produced a solution to this problem by recombining good traits from these two relatively fit parents into a superior (indeed, perfect) offspring. In summary, genetic programming has, in this example, automatically created a computer program whose output is equal to the values of the quadratic polynomial x2+x+1 in the range from –1 to +1.
· The home page of Genetic Programming Inc. at www.genetic-programming.com.
· For information about the field of genetic programming in general, visit www.genetic-programming.org
· The home page of John R. Koza at Genetic Programming Inc. (including online versions of most papers) and the home page of John R. Koza at Stanford University
· Information about the 1992 book Genetic Programming: On the Programming of Computers by Means of Natural Selection, the 1994 book Genetic Programming II: Automatic Discovery of Reusable Programs, the 1999 book Genetic Programming III: Darwinian Invention and Problem Solving, and the 2003 book Genetic Programming IV: Routine Human-Competitive Machine Intelligence. Click here to read chapter 1 of Genetic Programming IV book in PDF format.
· For information on 3,198
papers (many on-line) on genetic programming (as of June 27, 2003) by over 900
authors, see William
Langdon’s bibliography on genetic programming.
· For information on the Genetic Programming and Evolvable Machines journal published by Kluwer Academic Publishers
· For information on the Genetic Programming book series from Kluwer Academic Publishers, see the Call For Book Proposals
· For information about the
annual Genetic and
Evolutionary Computation (GECCO) conference (which includes the annual
GP conference) to be held on June 26–30, 2004 (Saturday – Wednesday) in Seattle
and its sponsoring organization, the International Society for Genetic and
Evolutionary Computation (ISGEC).
For information about the annual NASA/DoD Conference on
Evolvable Hardware Conference (EH) to be held on June 24-26
(Thursday-Saturday), 2004 in Seattle. For information about the annual Euro-Genetic-Programming
Conference to be held on April 5-7, 2004 (Monday – Wednesday) at the
University of Coimbra in Coimbra Portugal.
Last updated on August 27, 2003