Automatic Synthesis of Parameterized Topologies by Means of Genetic Programming
Genetic programming can automatically create a general solution to a problem in the form of a parameterized topology. That is, genetic programming can automatically create, in a single run, a general (parameterized) solution to a problem in the form of a graphical structure whose nodes or edges represent components and where the parameter values of the components are specified by mathematical expressions containing free variables.
In a parameterized topology, the genetically evolved graphical structure represents a complex structure (e.g., electrical circuit, controller, network of chemical reactions, antenna, genetic network). In the automated process, genetic programming determines the graph’s size (its number of nodes) as well as the graph’s connectivity (specifying which nodes are connected to each other). Genetic programming also assigns, in the automated process, component types to the graph’s nodes or edges. In a circuit, the component types are usually transistors, resistors, and capacitors. In a controller, the components are integrators, differentiators, gain blocks, adders, subtractors, and the like. Most importantly,. in the automated process, genetic programming also creates mathematical expressions that establish the parameter values of the components — that is, mathematical expressions that establish the capacitance of a capacitor and resistance of resistor in a circuit or mathematical expressions that establish the amplification factor of a gain block or the time constant of a lag block in a controller). Some of these genetically created mathematical expressions contain free variables (i.e., external inputs). The free variables confer generality on the genetically evolved solution by enabling a single genetically evolved graphical structure to represent a general (parameterized) solution to an entire category of problems. The important point about parameterized topologies is that genetic programming can do all the above in an automated way in a single run.
Example of a Parameterized Topology for a Lowpass Filter
As an example, suppose the goal is to design a circuit to feed the woofer speaker of a hi-fi system. That is, the desired circuit is intended to pass signals below a certain frequency at full power into the woofer, but to suppress all higher frequencies. Moreover, suppose that you want a general solution to this design problem. That is, suppose you want a solution that works for any cutoff frequency F1—not just a solution that works for, say, a value of 1,000 Hertz for F1. The figure below shows a genetically evolved general solution to this problem in the form of a parameterized topology.
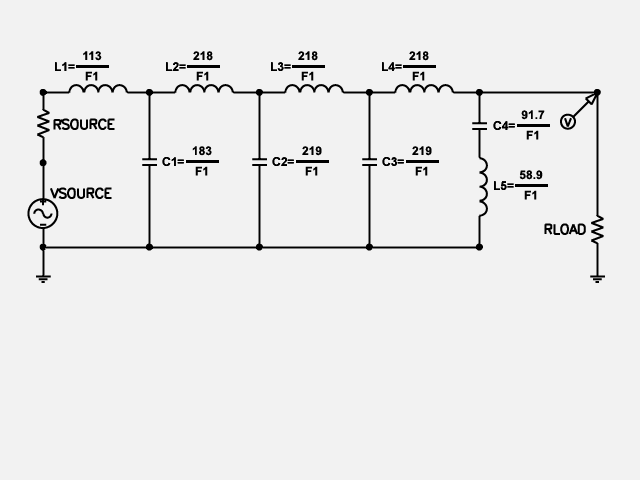
This general solution produced by genetic programming includes the circuit’s overall topology. The topology of a circuit, in turn, includes several aspects of the circuit, For example, the genetically evolved parameterized topology has a total of 9 components. The general solution includes the type of each of the 9 components — that is, there are 4 capacitors and 5 inductors. The connections between the 9 components are also automatically created during the run of genetic programming. The problem’s free variable, F1, is an input to the genetically evolved solution. The genetically evolved solution is general because the capacitance of the circuit’s 4 capacitors and the inductance of the circuit’s 5 inductors are not constant, but instead, are functions of the free variable F1. Specifically, the general solution produced by genetic programming includes 9 different mathematical expressions—each containing the free variable F1. For example, one of the 9 mathematical expressions specifies that the inductance of inductor L1 is 113/F1. When all 9 mathematical expressions are instantiated with a particular value of the free variable, the resulting circuit is a lowpass filter whose passband boundary is F1. Note that the numerical values of some components could be constant (although none of the values happen to be constant in this particular case). The advantage of a parameterized topology is it is a general solution to the problem—not just a solution to a single instance of the problem. Click here for an animated gif showing the different numerical values for the circuit’s 9 components for 5 different instantiations of values of the free variable, F1.
Example of a Parameterized Topology for a General-Purpose Controller
This example involves a general-purpose controller that is parameterized by 4 free variables, namely the plant’s ultimate gain, Ku; ultimate period, Tu; dead time, L; and time constant, Tr. Click here for an animated gif showing a genetically evolved general-purpose controller. This genetically evolved controller also has two gain blocks (730 and 760) whose gain is expressed as an equation involving the four free variables that describe a particular plant (i.e., Ku; Tu; L; and Tr). Specifically, equation 31 specifies the gain of gain block 730 and equation 34 specifies the gain of gain block 760.
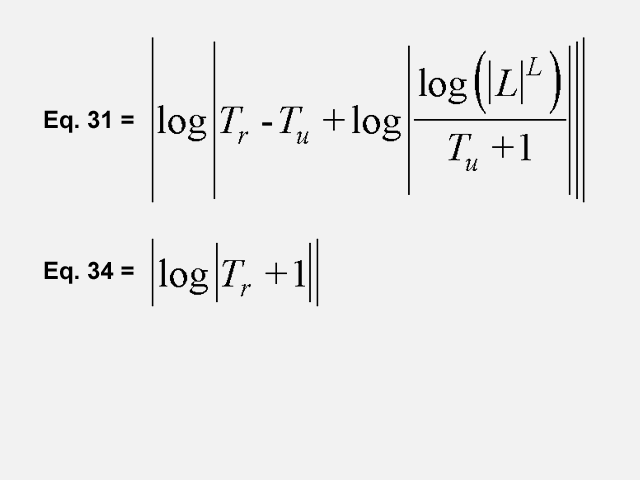
This genetically evolved controller also has two lead blocks (i.e., blocks with transfer functions of the form 1+ts) that are parameterized by genetically evolved mathematical expressions. Equation 32 specifies the numerical parameter of lead block 740. Equation 33 specifies the numerical parameter of lead block 750. NLM is a non-linear mapping (explained in the 2003 book Genetic Programming IV: Routine Human-Competitive Machine Intelligence).
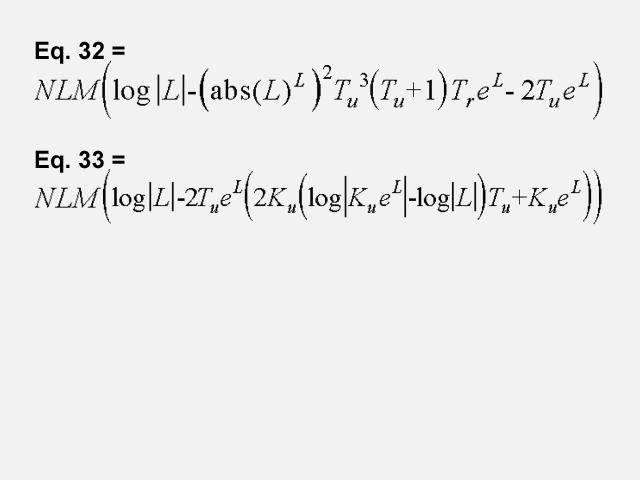
Example of a Parameterized Topology for a Circuit-Constructing Program Tree Containing Conditional Developmental Operators
Genetically evolved parameterized topologies may contain conditional operators. If the genetically evolved program contains conditional developmental operators, different graphical structures will, in general, be produced for different instantiations of the free variable. That is, the genetically evolved program will operate as a genetic switch. Depending on the values of the free variable, different graphical structures will result from the execution of the genetically evolved program. The numerical values for all parameterized components in the graphical structure will also be established by the execution of the program.
For example, suppose the goal is to automatically create a circuit-constructing program with free variables and conditional developmental operators that yields either a lowpass filter with a particular passband boundary or a highpass filter with a particular passband boundary. Suppose that the inputs to the program tree are the boundary of the passband (F1) and the boundary of the stopband (F2). Two functionally and topologically different circuits (lowpass versus highpass filters) are created depending on the particular values of two free variables. The boundaries of the passband and the stopband may vary over the range between 1,000 Hz and 100,000 Hz. The program’s inputs are the boundary of the passband (F1) and the boundary of the stopband (F2). If F1<F2, then a lowpass filter is desired, whereas if F2<F1, then a highpass filter is desired. Both desired filters are to have stopband attenuation of 60 decibels (1,000-to-1). When the inputs call for a highpass filter (that is F1>F2), the genetically evolved circuit has 6 capacitors and 6 inductors. The genetically evolved structure has 12 genetically evolved mathematical expressions. Click here for an animated gif showing the different numerical value of the circuit’s 12 components for 5 different instantiations of values of the free variables when inputs call for a HIGHPASS filter. When the inputs call for a lowpass filter (that is F2>F1), the genetically evolved circuit has 4 capacitors and 5 inductors. The genetically evolved structure has 9 genetically evolved mathematical expressions. Click here for an animated gif showing the different numerical values of the circuit’s 9 components for 5 different instantiations of values of the free variables when the inputs call for a LOWPASS filter.
11 Example of Parameterized Topologies
The capability of genetic programming to automatically create parameterized topologies is demonstrated in the 2003 book Genetic Programming IV: Routine Human-Competitive Machine Intelligence by the automatic synthesis of
· a parameterized controller
for controlling a three-lag plant whose time constant is specified by a free
variable (section 9.1),
· a parameterized controller
for controlling plants belonging to two different families (section 9.2),
· three parameterized
controllers for controlling industrially representative plants (chapter 13),
· a parameterized
circuit-constructing program tree containing two free variables that yields a
Zobel network (section 10.2),
· a parameterized circuit-constructing
program tree that yields a passive third-order elliptic lowpass filter whose
modular angle is specified by a free variable (section 10.3),
· a parameterized
circuit-constructing program tree that yields an active lowpass filter whose passband
boundary is specified by a free variable (section 10.5),
· a parameterized
circuit-constructing program tree that yields a passive lowpass filter whose
passband boundary is specified by a free variable (section 10.4),
· a parameterized circuit-constructing
program tree containing conditional developmental operators and
free variables that yields either a lowpass
or highpass passive filter (section 11.1),
· a parameterized
circuit-constructing program tree containing conditional developmental operators and
free variables that yields either a lowpass
passive filter with a variable passband boundary or a highpass passive filter with a variable passband boundary
(section 11.2),
· a parameterized
circuit-constructing program tree containing conditional developmental operators and
free variables that yields either a
quadratic or cubic computational circuit (section 11.3), and
· a parameterized
circuit-constructing program tree containing conditional developmental operators and
free variables that yields either a 40
dB or 60 dB amplifier (section 11.4).
· The home page of Genetic Programming Inc. at www.genetic-programming.com.
· For information about the field of genetic programming in general, visit www.genetic-programming.org
· The home page of John R. Koza at Genetic Programming Inc. (including online versions of most papers) and the home page of John R. Koza at Stanford University
· Information about the 1992 book Genetic Programming: On the Programming of Computers by Means of Natural Selection, the 1994 book Genetic Programming II: Automatic Discovery of Reusable Programs, the 1999 book Genetic Programming III: Darwinian Invention and Problem Solving, and the 2003 book Genetic Programming IV: Routine Human-Competitive Machine Intelligence. Click here to read chapter 1 of Genetic Programming IV book in PDF format.
· For information on 3,198
papers (many on-line) on genetic programming (as of June 27, 2003) by over 900
authors, see William
Langdon’s bibliography on genetic programming.
· For information on the Genetic Programming and Evolvable Machines journal published by Kluwer Academic Publishers
· For information on the Genetic Programming book series from Kluwer Academic Publishers, see the Call For Book Proposals
· For information about the
annual Genetic and
Evolutionary Computation (GECCO) conference (which includes the annual
GP conference) to be held on June 26–30, 2004 (Saturday – Wednesday) in Seattle
and its sponsoring organization, the International Society for Genetic and
Evolutionary Computation (ISGEC).
For information about the annual NASA/DoD Conference on Evolvable
Hardware Conference (EH) to be held on June 24-26 (Thursday-Saturday),
2004 in Seattle. For information about the annual Euro-Genetic-Programming
Conference to be held on April 5-7, 2004 (Monday – Wednesday) at the
University of Coimbra in Coimbra Portugal.
Last updated on August 27, 2003